几何学中，中位线定理是平面几何的一个重要定理，具有广泛的应用价值，本文旨在深入探讨中位线定理的内涵、证明方法及其应用，为读者呈现一个全面而深入的“中位线定理专题”。

中位线定理的定义与性质

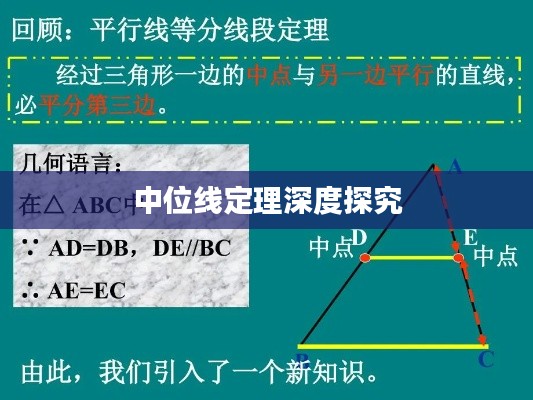
中位线定理：在三角形中，从一个顶点到对应的中点的线段，与这个顶点的对边相交，并且被该对边分成两段相等的线段，换言之，在三角形ABC中，若点D为边BC的中点，则AD将线段BC分为两段相等的线段BD和DC。

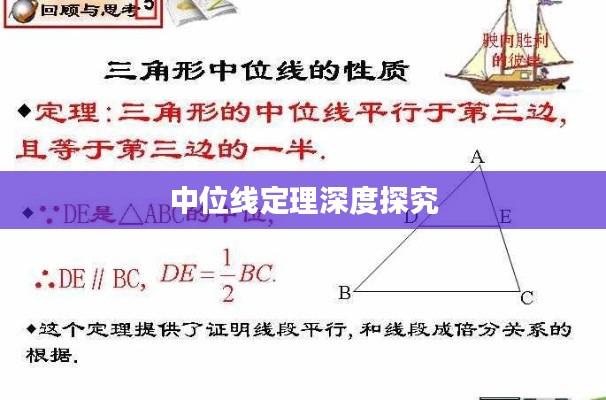
中位线的性质：中位线是三角形的一个重要特征，具有许多重要的性质，三角形的中位线平行于对应的对边，并且等于对边的一半，三角形的三条中位线相交于一点，称为三角形的重心。

中位线定理的证明方法

1、几何证明法：通过几何图形的性质和关系来证明中位线定理，这种方法直观易懂，但可能较为复杂。

2、代数证明法：利用代数方程和公式来证明中位线定理，这种方法严谨且适用于教学，但可能对初学者来说较为抽象。

中位线定理的应用

1、在求解三角形的问题中，中位线定理是求解线段长度、角度大小等问题的重要工具，已知三角形中的一边及其对应的中点，可以通过中位线定理求出其他边的长度或角度。

2、中位线定理在平面几何、数学物理、工程等领域有广泛的应用，在建筑工程中，利用中位线定理可以计算建筑物的稳定性和安全性，在数学物理中，中位线定理可用于求解力学问题、电磁问题等。

中位线定理的拓展与延伸

1、塞瓦定理：在一个凸四边形中，如果从两个对角分别引出两条中线，则这四条中线交于一点，该点称为四边形的重心，这个定理可以视为中位线定理的拓展。

2、在球面三角形中，也有类似的中位线定理，在球面三角形中，从一个顶点到对应的中点的线段与这个顶点的对边相交，并且被该对边分成两段相等的圆弧。

实例解析

为了更好地理解中位线定理的应用，我们来看几个实例：

例1：在三角形ABC中，已知AB=8cm，D为BC的中点，且AD将BC分为两段相等的线段BD和DC，求BD的长度，解：根据中位线定理，BD是BC的一半，所以BD=BC/2=AB/2=4cm。

例2：在四边形ABCD中，E和F分别是AB和CD的中点，求证：EF与对角线AC相交于一点，证明：根据塞瓦定理，我们知道四边形的四条中线交于一点，所以EF与对角线AC相交于一点。

本文详细探讨了中位线定理的定义、性质、证明方法及应用，并通过实例解析使读者更好地理解和掌握中位线定理，还介绍了中位线定理的拓展与延伸，如塞瓦定理和球面三角形中的中位线定理，希望本文能对读者在几何学的学习和研究中有所帮助。

参考文献

[此处插入参考文献]

附录

[此处可以添加一些与本文相关的图表、公式等辅助材料]

致谢

感谢读者阅读本文，希望本文能对读者在几何学的学习和研究上有所帮助，感谢同行专家和学者的支持与指导。